The CM Exception
Let us explore the Sato-Tate conjecture for this elliptic curve: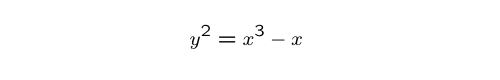
Obviously, those numbers do not satisfy the sin2 law. Indeed, some
elementary number theory shows that if the prime number p is of the form 4n+3,
then the equation y2 = x3 - x has exactly p solutions mod p,
so that ap=0. This means φp=π/2 and explains the prominent spike in the middle.
What is going on? The explanation is that the above elliptic curve belongs to a small exceptional class called CM elliptic curves, where CM stands for complex multiplication. For this class, the Sato-Tate conjecture is not supposed to hold.
What is going on? The explanation is that the above elliptic curve belongs to a small exceptional class called CM elliptic curves, where CM stands for complex multiplication. For this class, the Sato-Tate conjecture is not supposed to hold.
Finally, check out the notes and references on page 5.
