

The Fibonacci series is a famous example of an object with a simple mathematical description, but a nearly inexhaustable list of bizarre and complicated properties. Originally, the series was described by Fibonacci in the 15th century in connection with the following problem:
Assume that a pair of rabbits will breed another pair of rabbits every month of their lives, after sexual maturity. Assume also that rabbits become sexually mature after two months. Starting with one newborn pair of rabbits, describe how many rabbits you get in successive months.
At the end of the first month you have 1 pair. After another month, you still have 1 pair. However, at the end of the third, the first pair has become sexually mature, and produced offspring, so you have 2 pair. At the end of the next month, the first pair reporduces again, while the second pair remains immature, so you have a total of 3 pair.
Proceeding in this fashion, one sees that the following list of numbers describes the breeding of the rabbits:
1,1,2,3,5,8,13,21,34,55,89,144,...
The decimal expansion of 1/89 is just the Fibonacci series, added together in an appropriate fashion.
Specifically, think of the Fibonacci series as being a sequence of decimal fractions, arranged so the right most digit of the nth Fibonacci number is in the n+1th decimal place. Then add:
.01
.001
.0002
.00003
.000005
.0000008
.00000013
.000000021
.0000000034
.00000000055
.000000000089
.0000000000144
.
.
+ .
----------------
.01123595505...
As you can easily check, 1/89 = .01123595595... Bizarre, eh?

Proof. Consider the matrix
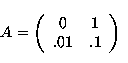
Note that
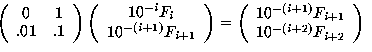
Consequently, it follows that
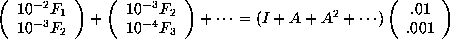
On the other hand, by diagonalizing A, one easily checks that the geometric series converges, and in fact,
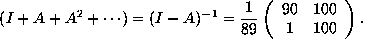
Thus
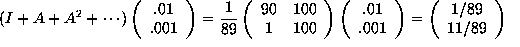
The result now follows.